Protein Synthesis (part 2): Grade 9 Understanding for IGCSE Biology 3.18B

In the last post, I asked you to think of a good “2 mark” explanation of some important terms to do with protein synthesis.  Here is my (GCSE level) answer…..

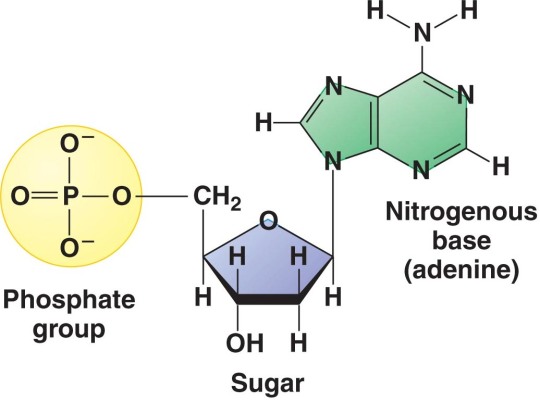
Gene: “a section of a DNA molecule that codes for the production of a single protein”

Ribosome: “a small structure found in the cytoplasm of cells where proteins are made by joining amino acids together into a long chain”

Transcription: “the process occurring in the nucleus in which a double-stranded DNA molecule is used to make a single-stranded molecule of messenger RNA”

Messenger RNA: ” a small single stranded molecule that is made in transcription and can carry the genetic information out of the nucleus to the ribosome”

Translation: “the second stage of protein synthesis that occurs in the cytoplasm in a ribosome in which amino acids are joined together in the correct order to make the protein”

Codon: “a triplet of adjacent bases in an mRNA molecule that codes for a single amino acid”

2b597889d05bc601803a3b4d9ec5ccd5e7b8d3af

Finally I want to answer three important questions, one in this post, two in the next….

Why are codons three bases long?

Well, the answer here is a simple bit of Maths.  If you remember, there are 20 possible amino acids that can be joined together in any order and in any number to make a protein.  In DNA/RNA there are just four bases.  So in order to code for 20 amino acids, how many “words” do you need?  Well you need at least 20…..

In DNA/RNA you only have 4 “letters” available to make these words.  (The letters are the bases and the words are the codons.)

  • If the words were one letter long, there are only 4 words. (43 for the mathematicians):  A,T,C,G
  • If the words were two letters long, there are only 16 possible words (42 for the mathematicians): AA, AT, AC, AG, CA, CT, CC, CG, GA, GT, GC, GG, TA, TT, TC, TG
  • If the words were three letters long, there are 64 possible words (43 for the mathematicians)  AAA, AAT, AAC, AAG, ACA, ACT, ACC, ACG etc. etc.

So three bases in a codon is a minimum number needed to code for 20 different amino acids.  But then this raises a question, doesn’t it?  If there are 64 possible words and only 20 words needed, then what happens to all the extra, unnecessary codons?  The answer is that there are lots of synonyms in the language of DNA/RNA.  (Synonyms are two different words that have the same meaning)

Check out this picture of the genetic code (written in the language of RNA) and notice all the lovely synonyms!

GeneticCode

Phe, Leu, Ser, Tyr, Cys and the others are names of amino acids

Notice that almost all amino acids have more than one codon that codes for them.  For example, the amino acid Thr (threonine) is coded for by ACU, ACC, ACA and ACG in mRNA.

The three codons marked STOP are used as signals for the ribosome to stop the process of translation (but you don’t need to worry about that unless you wisely choose to continue your studies in Biology at A level!)

This is complicated stuff so please feel free to ask me questions about this using the “leave a comment” box below.  You won’t get an instantaneous response but I try to check my blog every couple of days.

RNA: Grade 9 Understanding for IGCSE Biology 3.17B

You need to understand the structure of the molecule DNA before you read this post.

DNA stands for deoxyribonucleic acid and is the chemical that makes up the genetic information in all living organisms on earth.  DNA is a double-stranded molecule in which each strand is made of a polymer of simple molecules called nucleotides.  There are four nucleotides in DNA, with each nucleotide differing in the base present in the molecule.  Adenine, Thymine, Cytosine and Thymine are the four bases found in the nucleotides in DNA.  Every nucleotide in DNA contains the same sugar, deoxyribose and a phosphate group as shown in the diagram below.

 

But DNA is not the only nucleic acid found in cells.  All living cells also contain a similar molecule RNA that serves a whole variety of different functions.  It is not the main genetic material in any cell but is essential in allowing the information contained in a DNA molecule to be expressed as a protein (see post on protein synthesis to come)

RNA stands for Ribonucleic Acid and is also a polymer of nucleotides.  But whereas DNA is always a double-stranded molecule, RNA is always single-stranded (although certain forms of RNA can fold back on themselves at points so they can appear double stranded).  The sugar in every RNA nucleotide is ribose (as opposed to deoxyribose in DNA).

25-31a.JPG

There are also four different bases found in RNA nucleotides.  Three are identical to the bases found in DNA (Adenine, Cytosine and Guanine) but there is no Thymine in RNA.  RNA can contain nucleotides with the similar base Uracil in its place.

what-are-the-key-differences-between-dna-and-rna-296719

So in summary:

  • RNA is single stranded whereas DNA is double stranded
  • RNA contains the sugar ribose in every nucleotide whereas DNA contains deoxyribose
  • DNA contains 4 bases (ATCG) whereas RNA contains A,U,C and G (thymine is replaced by uracil)

Protein Synthesis (part 1): Grade 9 Understanding for IGCSE Biology 3.18B

This is by far the most difficult concept for you to understand in the new GCSE specifications. In fact, it was only ever taught to A level students until last year (and to be honest I would much prefer it that way!). But that is no consolation to you poor folk who are going to get tested on it in your IGCSE and GCSE exams…

I am going to keep this as simple as I possibly can but am not going to dumb it down…. My blog is aimed for students who are ambitious to develop Grade 9 understanding in Biology (this topic is not tested at all in our Double Award Science course) so I want to explain it to you at the level you need.  But you will need to read this carefully, take your time and you might need to break it down into small sections to build the understanding you need.

Can I suggest that first of all you read this post from my blog about DNA and how it works?

What is a gene?

A gene is a section of DNA that codes for a single protein.  How does this code work?  Well the short answer is that the sequence (order) of the bases as you read along the DNA molecule is a code for the sequence of amino acids that are joined together to make the protein.

Remember that there are 4 different bases in DNA: Adenine (A), Thymine (T), Cytosine (C) and Guanine (G).  So a sequence of bases on a piece of DNA might look like this:

GCCTATAAATGGCAGGCATTAGCTCTAGGAAATCTAGGGACTTTACA

Protein Synthesis

Proteins are made by joining small molecules called amino acids together.  This process is called protein synthesis and happens in small structures in the cytoplasm of all cells called ribosomes.  But for all eukaryote cells, this poses a big geographical problem.

The “information” in the gene is stored in a sequence of bases in a DNA molecule and is found in the nucleus.  DNA never leaves the nucleus because it is too important a molecule to be allowed into the reactive and unpredictable environment in the cytoplasm.  But there are no ribosomes in the nucleus and these are the structures in which proteins are actually made.  So a temporary intermediate molecule is needed to carry the “information” from the gene in the nucleus out into the cytoplasm where the ribosomes are found.  So the process of making a protein therefore has to exist as a two stage process.  The first stage is making the temporary intermediate molecule using the sequence of bases in the gene.  Then there is a second stage that happens in the cytoplasm in the ribosome and this involves joining the amino acids together to make the actual protein.

This idea was called the “central dogma of molecular biology” by Watson and Crick in their famous paper on the structure of DNA.

central-dogma.jpg

Transcription and Translation

There is quite a lot of jargon in this topic.

Transcription is the name for the process that happens in the nucleus in which a temporary intermediate molecule is made.  This temporary “information-containing” molecule is a form of RNA called messenger RNA (or mRNA for short).  The mRNA travels out of the nucleus to a ribosome which is found in the cytoplasm.  Here a process called Translation occurs in which the the amino acids are joined together in the correct order to make the protein.

2b597889d05bc601803a3b4d9ec5ccd5e7b8d3af

Look at this second diagram of the central dogma above.  It shows a double-stranded DNA molecule at the top with pairs of bases (either A-T or C-G) joined by hydrogen bonds.  The “information” in the molecule is found in the sequence of bases: on the top strand of the DNA this sequence is ATGATCTCGTAA.

You can see that transcription results in the formation of a molecule of mRNA.  (Remember that RNA is always a single stranded molecule and contains the base Uracil in place of the base Thymine)

So can you see that the sequence of bases in the mRNA is almost identical to the DNA strand above, but with the base T replaced by the base U.

mRNA sequence:  AUGAUCUCGUAA

This diagram shows us one final thing about how protein synthesis works.  Look now at the small section of protein (polypeptide) that is produced in translation.  You can see that this section of protein is made of three amino acids joined together:  methionine (Met), attached to isoleucine (Ile) attached to serine (Ser)

Each amino acid is coded for by a group of 3 adjacent bases on the mRNA molecule.  These triplets of bases are called Codons.

  • AUG is a codon that codes for the amino acid Methionine
  • AUC is a codon that codes for the amino acid Isoleucine
  • UCG is a codon that codes for the amino acid Serine

(UAA is called a stop codon as it ends the translation process at the ribosome)

A codon is a triplet of adjacent bases on a mRNA molecule.  Each codon codes for a single amino acid that will be joined together to make the protein.

Check your understanding:

Can you explain the meaning of the following terms?  Write a 2 mark explanation of what each word means.

  1. Gene
  2. Ribosome
  3. Transcription
  4. Messenger RNA
  5. Translation
  6. Codon

I will put the answers into the next post called Protein Synthesis (part 2) which I promise I will write tomorrow…… That’s enough for now.

 

Stem Cells in Medicine: Grade 9 Understanding for IGCSE Biology 2.6B

In the previous post, I described what is meant by a stem cell and how stem cells are formed from the non-specialised cells of the embryo in a process called differentiation.

Stem cells have the potential to be used in a variety of medical treatments.  At present, there are very few diseases for which stem cell treatments are available in the UK but the potential is certainly there for many more in the future.

stem-cell-uses.png

What are the advantages of using stem cells in medicine?

Many diseases in the body are caused by certain groups of cells dying prematurely.  For example Parkinson’s Disease is a brain disease where a small group of nerve cells in the substantia nigra of the brain die.  Diseases like this are called degenerative diseases and some examples are shown in the diagram above.  Stem cells allow the possibility of replacing the cells that have died with new cells derived the patient’s own stem cells.  The big advantage of doing this (as opposed to replacing the lost cells with transplanted cells from another person) is that there should be no chance of the immune system rejecting the transplanted cells.  If scientists could take some of the patient’s adult stem cells and treat them so they become specialised into new substantia nigra cells,  these cells could be added into to the brain and the symptoms of the disease may be overcome.  This offers a cure to some diseases that are currently very difficult to treat.

What are the disadvantages of using stem cells in medicine?

But…….  the main problem is this.  Adult stem cells (such as those found in the bone marrow) are multipotent.  This means that they can only develop into a small number of cell types.  To get pluripotent stem cells that can develop into almost all cell types, you need to get the stem cells from an embryo.  These stem cells are much more useful for doctors and usually comes from “spare” embryos produced in IVF treatment for infertile couples.  This leads to serious ethical implications as the early embryo of course cannot give informed consent to be used in this way!  There are also practical difficulties.  Stem cells have the potential to develop into tumours when put into the body and thus cause cancers.  They may also provide a way for dangerous pathogens to get into the body.   Embryonic stem cells may also be rejected by the patient’s own immune system and killed.

If you want to watch a summary video about stem cells, this is a good one in my opinion.

 

Cell Differentiation and Specialised Cells: Grade 9 Understanding for IGCSE Biology 2.5B

You will have learned at KS3 about the basic structure of a “typical” animal cell.  But our bodies are not made of cells that look like this “typical” cell.  Humans have just over 200 different types of cell, each specialised to carry out a particular function.  For example red blood cells are specialised for transporting oxygen, muscle cells are specialised for movement and sperm cells are specialised as the male gamete for delivering a haploid nucleus to the egg cell.

specialised cells

The diagram above shows examples of a few types of specialised cells from the human body.

These specialised cells are produced in the process of cell division.

cell division.jpg

Cells that are not yet specialised but that retain the ability to develop into a variety of different cell types are called stem cells.   Many cells in the embryo are stem cells (as they have not yet specialised into a particular cell type) but we also have a few stem cells in the adult (for example the cells in the bone marrow that can develop into all the different cell types in blood).

600px-Final_stem_cell_differentiation_(1).svg

The process by which stem cells develop into specialised cells is called differentiation.  Luckily you don’t need to understand exactly how this works but basic idea is this:  differentiation involves certain genes in the nucleus being switched on and off so that a specialised cell only makes a certain set of proteins.  Remember that a gene is a section of our DNA that codes for a single protein.  Nerve cells make the proteins needed to send nerve impulses, white blood cells make the proteins needed to combat infections.  You get the idea…..

cell-differentiation

Stem cells play an important role in medicine but that’s for another post………  If you want to read more about stem cells, this website is a good place to start.

2019 EdExcel Biology IGCSE Updates

I haven’t had much time to work on my IGCSE Biology revision blog lately – life seems a bit more busy – but the summer holiday does give me time to sit in front of the computer and work on my blog.

I have been through the new specification and can see there are some “gaps” that I need to fill.  So please look out for posts on the following specification points:

  • Cell Differentiation and Stem Cells 2.5B, 2.6B
  • Balanced Diets and Energy Requirements 2.25, 2.26
  • Stomata, Leaves and Gas Exchange 2.42B, 2.43B, 2.44B
  • Transpiration and the environmental factors that affect it 2.56B, 2.57B, 2.58B
  • Nervous v Hormonal Communication comparison 2.86
  • Hormones 2.94, 2.95B
  • Hormones of the Menstrual Cycle 3.9, 3.10B, 3.13
  • DNA, RNA and Protein Synthesis 3.16B, 3.17B, 3.18B
  • Determination of Sex of Offspring 3.26, 3.27
  • Fermenters and Industrial Culturing of Microorganisms 5.8

If these posts haven’t appeared by September, please contact me by leaving a comment below and give me a “nudge”!

In the meantime, happy holidays!!

image_preview

Two days to go before the EdExcel IGCSE Biology paper 2

I’m writing this on Friday evening and the 2018 IGCSE Biology paper 2 is on Monday.  So you are almost there…..

What can you do in the final two days?

  1. Look over the topics that can only appear in paper 2 and make sure you understand them as well as you can.
  2. Look at my post with some guesses as to what topics were not assessed on paper 1 and make sure you understand them as well as you can.
  3. One last work through those topics in the specification where you know your knowledge or understanding is not great (don’t waste time this weekend going over things you definitely already understand!)
  4. Rest properly, get two proper nights’ sleep so you are relaxed and ready to THINK in the exam on Monday.  You will need some downtime this weekend to enjoy yourself and switch off thinking about exams…..

Good luck to you all!  Your study of GCSE Biology is almost over… I will have my fingers crossed that the exam paper on Monday allows you to demonstrate the detailed knowledge and understanding you have built up

Genetics follow up: Grade 9 understanding for IGCSE Biology 3.19 3.20 3.21B

In an earlier post, written for my own Y11 students at a previous school, I asked them to check that they knew the answers to 5 questions before attempting to answer any practice questions involving inheritance and genetics. I think that as this blog is now read by a much wider audience, it is probably time to answer the 5 questions myself! Here goes……

1) What is the difference in meaning between a gene and an allele?

People who I have taught know that there is just one thing that every A* student should memorize for IGCSE Biology and that is the definition of a gene.

“A gene is a sequence of DNA that codes for a single protein”

Genes are located on chromosomes and exist in alternate versions called alleles. So for example in pea plants there is a gene that codes for a protein that determines the height of the pea. This gene exists in two possible versions: a T version that makes the plant tall and a t version that makes the plant short. These alternate versions of a single gene are called alleles.

2). Why does the genotype of a person, plant or rabbit always contain two alleles for each gene?

In order to understand this, you need to understand something about chromosomes. Humans, plants and rabbits are all diploid organisms – this means that they have pairs of chromosomes one inherited from mum, one from dad. Because genes are found on chromosomes, this means that a genotype (combination of alleles) will also have two alleles. Alleles are versions of genes, genes are found on chromosomes and chromosomes come in pairs! Simple…

3) What is different about the genotype of a gamete compared with other body cells? Why are gametes different?

Gametes only contain one allele for each gene. This is because gametes are cells that do not contain pairs of chromosomes like every other cell in the body. Gametes are haploid – they only have one member of each pair of chromosomes. One chromosome per pair means only one version of each gene…. Gametes have to be different because they have a different fate or destiny to every other body cell. (Just typing the word destiny means I can hear the Star Wars theme as clear as anything in my head!). Luke’s destiny was to unite the light and dark sides of the force. A gamete’s destiny is less exciting but it is to fuse with another gamete in the act of fertilisation. If both gametes had pairs of chromosomes like every other body cell, then the act of fertilisation would result in a doubling of the chromosome number in every generation and that is clearly unlikely to do anyone any good!

4) How would you explain what is meant by a recessive allele?

A recessive allele is always given the lower case symbol, for example t. The best way to explain what is meant by a recessive allele is to say that recessive alleles only determine the phenotype (the appearance of the organism) if there are two of them. An individual with two identical alleles for a gene is described as being homozygous so a recessive allele will only determine the phenotype in a homozygous individual. In the example I have used so far, because the dwarf allele, t is recessive, the only genotype possible for a short pea plant is tt.

5) What does it mean if two alleles are codominant?

Codominant alleles are alleles that both contribute to the phenotype in a heterozygous individual. Heterozygous is the adjective used if the two alleles present are different to each other.

A good example is the genetics of the ABO blood group system in humans. There are three possible alleles present for this gene in the human population: IA, IB and IO.

The IA allele is dominant to the IO allele.

The IB allele is dominant to the IO allele.

But if you are heterozygous with the genotype IAIB then you have an intermediate blood group called AB. Both alleles are contributing to your blood group and so you are neither blood group A, nor blood group B but a different phenotype called AB. This is because the alleles IA and IB are codominant to each other.

This is a complex topic (not tested at all in the 2018 Paper 1B) so it is worth trying to get your head around all the jargon here over half term…….

If you have any questions at all, please ask me in the “Leave a Comment” box at the foot of this post.

EdExcel IGSE Biology Paper 2B 2018 predictions

I hope readers of my blog felt that the Biology paper 1B went well earlier this week.  For what it is worth, I thought it was a good but challenging paper but there is nothing at all on there that seemed unfair to me.  I am confident that it gave students a good chance to show the understanding and knowledge you have built up over three years.  But…..   you still have 33% of your marks still available to you, so my thoughts have now turned to paper 2B in a few weeks time.

I have been through the paper 1B carefully to look at which subject areas have been tested in the questions. This might allow you to focus your revision now onto topic areas that have not yet come up.  But the next point is very important:  there is absolutely nothing that says they cannot ask questions on the some of the same topics inboth papers.  Predicting exam questions is a dangerous game (!?!) and there is absolutely nothing in this blog post that should contradict the idea that you need to be fully clued up and ready for questions on every single specification point when you sit your paper 2B.

But there are some things we know about what is likely to appear in the paper 2B.

  • Firstly there are some specification points in bold that cannot be assessed in paper 1 and can only appear in paper 2.  I have a blog post that lists these so I won’t type them all out again.  Have a look here to see a full list of the bullet points in bold….
  • Listed below are some topic areas that were not tested at all in the summer 2018 paper 1B.  I would anticipate that several of these will definitely appear in paper 2B so if I were in your position, these would be my top priorities for revision in the coming weeks:

Variety of Living organisms and 5 Kingdom Classification 1.2

Viruses 1.2

Movement of substances into and out of cells – Diffusion, Osmosis and Active Transport  2.12, 2.13, 2.14, 2.15, 2.16

Transport in Plants – Xylem and Phloem 2.51, 2.52, 2.53, 2.54, 2.55. 2.56

Heart Structure and Circulatory Systems 2.63, 2.64, 2.65, 2.66

Human Nervous Systems 2.83, 2.84, 2.85, 2.86,

The Eye 2.87, 2.88, 2.89,

Hormones 2.90

Reproduction in Flowering Plants 3.3, 3.4, 3.5, 3.6, 3.7

Reproduction in Humans 3.8, 3.9, 3.10, 3.11, 3.12

DNA and Genetics – this must come up!!  3.13, 3.14, 3.15, 3.16, 3.17, 3.18, 3.19, 3.20, 3.21, 3.22

Ecology – Food chains and Webs, quadrats etc. 4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7

Carbon and Nitrogen Cycles 4.8, 4.9, 4.10

Selective Breeding 5.10, 5.11

Genetic Modification 5.12, 5.13, 5.14, 5.15, 5.16

Cloning 5.17, 5.18, 5.19, 5.20

The focus of your revision now should be looking at past papers and mark schemes.  I know many of you have done this already for paper 1B.

If you want more past papers and mark schemes, I suggest you download them for free from this website: http://www.physicsandmathstutor.com/past-papers/gcse-biology/edexcel-igcse-paper-2/

Please remember there are posts on my website for every single specification point above.  Just type in the specification code in the search box and it should (?!) take you straight to the relevant page.  Please do ask me questions or leave comments at the bottom of any posts.  It may take a while for them to be visible as I have to “approve” them to remove spam.  You would be amazed at some of the stuff I seem to attract from the depths of the internet…..

Keep working hard and good luck!

 

 

How best to organize your revision time in the Easter holidays: some PMG tips

Tomorrow is the first day of the 2018 Easter holidays and so it is definitely a good time for Y11 students to think about how they are going to make the most effective use of the time available for revision.  I know that everyone works differently but I thought I would write a post to give you something to think about….  Please leave a comment at the end of this post if you find any of this useful.

Starting Points:

Easter holidays are a critical time for Y11 students.  The IGCSE and GCSE specifications contain so much content that the challenge for you is mostly one of being on top of so much material come exam day.  And your exams arrive so early in the summer term that there won’t be much time when you get back to school after the holidays.  So it has to be now! (The summer will be very long and there will be plenty of time for lazy days when nothing at all happens…. )

The hardest thing about revision is getting started.  If you can build up some early momentum, you will be able to keep your energy and enthusiasm up right through the holidays.  So why not start tomorrow…..?

How to organise a revision plan

  • It is vital you have a plan.  A little time this evening or tomorrow morning spent on getting organized will be time well spent!  This would be how I would do it if I could rewind the clock to the summer of 1987….. U2 released The Joshua Tree that year and I thought at the time it was the greatest music ever made….
  • Speak to your parents tonight and ask them to talk you through what’s coming up in the holidays.  What family commitments do you have that will impact on your revision schedule?
  • Count up how many days you will be able to work between now and when school starts again.  For my current students, we have 25 days before term starts.  But I think you need a few days off at times in the coming weeks.  So let’s say, there may be 20 “work” days.
  • This is how I suggest you organise a “work day”…. You always do work in the morning session (9am-11.30am) and then you choose either the afternoon slot (2-4.30pm) or the evening slot (7.30pm – 10pm).  This is an ambitious schedule as 5 hours work in a day is quite a lot.  But let’s aim high!
  • Each session is divided into 5 periods of 30 minutes.  You must work on a different subject in each period in a session.  Have a plan before the session so you know exactly what you are going to achieve.  The next bit is very important.  At the start of the session, switch your phone off and put it in a different room.  Start a kitchen timer (not a timer on your phone obviously!) and set it to 25 minutes.  Work at your revision until the alarm goes off.  Then you get a 5 minute gap (tea/check Snapchat) before the next slot starts.
  • The PMG schedule has two huge advantages:  firstly you have completed half your work for the day by 11.30am (which feels good, believe me) and secondly you can enjoy the time you are not working without feeling guilty…. This is a key component to a successful revision programme. Work when you are supposed to be working but then do other stuff, see friends, do some exercise , watch tv, relax.  Revision isn’t effective if you are tired or bored so both must be avoided at all costs.

Many of you have 9 or 10 subjects to revise.  If we assume 10 subjects to revise (which makes the Maths easier) 20 work days in the holidays and 10 periods per day (see schedule above), this means that you have 20 periods per subject in the holidays.  Do the calculation with your numbers so you know how many revision tasks you need to plan per subject.    My example gives you 8 hours 20 minutes per subject – your job is to make the very best use of this time so you gain the most from it.  I wish you all the very best of luck and don’t forget to leave a comment below.  Happy revising!