Tagged: 2.27

July 26, 2019

The Human Alimentary canal: Grade 9 Understanding for IGCSE Biology 2.27

A human body is in many ways rather like a packet of polo mints. These are famous mints in the UK for having a hole in the middle. Our body is divided into segments (rather like the packet of polos) and we have a tube that runs through the middle of us. This tube is called the Alimentary Canal (or Gut) and it’s function in the body is the digestion and absorption of food molecules (see later post on “Stages of Processing Food”)

The Alimentary Canal is divided into specialised regions, each with its own particular range of functions to do with the processing of food. You are required to understand a little about some of these organs and their functions.

The first thing is to make sure you can label a diagram of the human digestive system such as the one shown above. Check that you could accurately identify the following structures:

mouth, tongue, teeth, salivary glands, oesophagus, stomach, liver, gall bladder, bile duct, pancreas, pancreatic duct, duodenum, ileum, colon, appendix, rectum, anus

Here is a good diagram to use to check your labelling of the human digestive system

Functions

1 Mouth

The mouth is actually the name for the opening at the top of the alimentary canal rather than the chamber behind. If you want to be really precise, you should call this chamber containing the tongue and teeth by its proper name, the buccal cavity. The mouth is the opening that allows an animal to ingest food. In the buccal cavity, the teeth can chop up the food into smaller pieces and the tongue can move the food into a ball (bolus) for swallowing. The food is tasted in the buccal cavity and there are many chemoreceptors on the tongue and in the nasal cavity that perform this function. There are three sets of salivary glands around the buccal cavity and these secrete a watery liquid, saliva to mix with the ingested food. Saliva is alkaline to help protect the tooth enamel from acidic decay by bacteria but also contains a digestive enzyme, salivary amylase that begins the process of digestion of starch in the mouth. Salivary amylase catalyses the hydrolysis reaction in which starch, a polysaccharide is digested into the disaccharide maltose.

2 Oesophagus

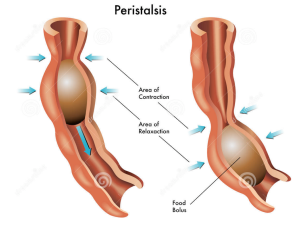
The oesophagus is the tube that carries the ball of food from the back of the throat through the thorax and down into the stomach. The Alimentary canal has layers of muscle in its wall throughout its entire length. These layers of smooth muscle can contract and relax in an antagonistic fashion to push the bolus along the tube. There are two main types of smooth muscle in the wall of the Alimentary canal – circular fibres are arranged around the circumference of the tube and longitudinal fibres are arranged along the length of the tube. These waves of alternate contraction and relaxation are called peristalsis.

3 Stomach

The stomach is a muscular storage organ that keeps food in it for around 3-4 hours before squirting it out in small amounts into the duodenum. The muscle layers in the stomach wall churn the food and mix it with the secretions from the stomach lining. These secretions are called gastric juice and contain a mixture of hydrochloric acid, mucus and a digestive enzyme pepsin. The acid makes the gastric juice overall very acidic, around pH 1.5. This acidity forms part of the non-specific defences of the body against bacteria as the extreme pH kills almost all bacteria in the food. The mucus is important as it protects the cells lining the stomach from the acidity. Pepsin is a digestive enzyme that starts the digestion of protein. It catalyses a hydrolysis reaction in which proteins are broken down into smaller molecules called polypeptides. Pepsin is an unusual enzyme in that it has an optimum pH of around 1.5.

4 Small Intestine

I will write a whole post on the small intestine later this week as there is plenty for you to understand about this part of the alimentary canal. All I will say here is that it is divided into the duodenum which is where almost all the digestion reactions take place and the ileum which is adapted for efficient absorption of the products of digestion into the blood. (see post later in the week if you want to find out more….)

5 Large Intestine

The majority of the large intestine is made up of an organ called the colon. The colon has a variety of functions. It is where water from all the various secretions is reabsorbed back into the blood, thus producing a solid waste called faeces. (Water that you drink tends to be absorbed through the stomach lining much earlier in the alimentary canal) There are also a few mineral salts and vitamins absorbed into the bloodstream in the colon. The colon is also home to a varied population of bacteria, the so called gut flora. Faeces is stored in the final part of the large intestine that is called the rectum.

6 Pancreas

The pancreas is not part of the alimentary canal (although I am not sure the person who wrote the specification appreciated that….) It is an example of what is called an accessory organ for the digestive system. The pancreas is a really interesting organ as it contains different cell types that carry out two completely separate functions. The majority of the cells in the pancreas secrete a whole load of digestive enzymes into an alkaline secretion called pancreatic juice. There is a tube called the pancreatic duct that carries the pancreatic juice and empties it into the duodenum where it can mix with the acidic chyme coming out of the stomach.

Pancreas+ text.indd

There are small clusters of a different kind of cell found in the pancreas. These are the islets of Langerhans that secrete the hormones insulin and glucagon into the bloodstream. These two pancreatic hormones together regulate the blood glucose concentration.

October 29, 2015

Stages in Processing Food: A* understanding of animal nutrition for IGCSE (no longer in specification)

Most animals including humans feed by a process called holozoic nutrition. This means that the animal has a gut tube (alimentary canal) that runs through its body and the animal has a mouth at one end (this is where the food goes in), an anus at the other end where undigested food (faeces) passes out.

Ingestion: the first stage of feeding involves food being taken up into the mouth (not too complicated to understand I hope…)

Most food is made up of very large molecules (macromolecules) such as starch, proteins and lipids. These molecules are too large to be absorbed from the gut tube into the blood. So the second stage of feeding involves chemically breaking down these large food molecules into smaller solubles molecules that can be absorbed.

Digestion: the chemical breakdown of large insoluble food molecules (e.g. proteins/starch/lipids) into smaller soluble molecules (amino acids/sugars/fatty acids and glycerol) that can be absorbed. Digestion is a chemical process and every digestive reaction is catalysed by a specific enzyme. Almost all these digestive enzymes are secreted into the gut tube and mixed in with the food. Please see a later post on Digestion to get a full understanding of these reactions.

Absorption: the small products of digestion are then absorbed into the blood stream. This process occurs almost exclusively in a region of the small intestine called the ileum. The structure of the ileum is beautifully adapted for efficient absorption – see a later post on Absorption for full details!

Assimilation: this is the stage of processing food that is sometimes left out. This is because it does not happen in the alimentary canal but instead in the body cells of the animal. The small soluble products of digestion (glucose, amino acids, fatty acids etc.) are taken up into cells and used to build the animal’s own macromolecules – proteins/lipids/glycogen etc. Assimilation is a term for how small molecules are built up and used in the cells of the animal.

Egestion: this is the final stage and involves undigested food, mostly cellulose in humans, being passed out of the anus as faeces at the end of the alimentary canal.

Don’t confuse egestion with excretion….. Egestion is simply passing out undigested food from the end of the large intestine. If you think of your body like a tube of polos (you know I do…) then the stuff that comes out of the large intestine has never actually been inside your cells. It is mostly cellulose and other plant fibres that went into the mouth a day or two ago, haven’t been digested nor absorbed and so come out the other end. Excretion on the other hand is the process of removing waste molecules that have been made inside cells. So the lungs removing carbon dioxide, the kidneys taking urea out of the blood to make urine – these are examples of excretion.

A slightly lavatorial way to end the post but important nonetheless: if you are talking about urine production, this is excretion, but “number twos” or “Richards” (look up cockney-rhyming slang for EAL speakers) are not excretion, they are egestion….